в третьем случае (рис. 14, в, г) при f о = О количество ДНС

Ni= I, а при Од = 1 =»- Л/а = П Следовательно,

=П(«/ + 1) + 1.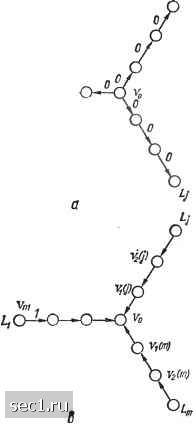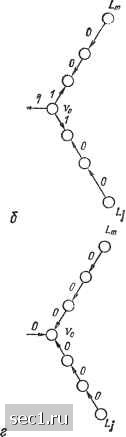

Рис. 14. Синдромы минимальных звездных структур

Таким образом, при объединении минимальных структур в звезду

Лп,1п = П(«/ + 0+ 1-/=-1

(3.9)

Интерес представляет здесь сравнение полученных оценок со случаем последовательно соединенных элементов.

Пусть «,-= {п - 1)/т, / = 1.....т является целым числом.

Тогда максимальное количество ДНС

/=1 / /=1 /

+ + /(п-l)/m-2 (n-l)/m-Л.

а минимальное определится как

ЛП,.П = f 1 (П; + 1) + 1 = 1)"+ 1.

Таким образом, при объединении в звезду, по сравнению с цепочными структурами, ухудшаются верхняя оценка Лтах и нижняя Nmin количсства ДНС. Так, при п = 13,

m = 4 для цепочной структуры Nax = /13= 610, Nnnn= 14,

а для звездной структуры

тах = ifn-U/m-ir + (/(n-D/m)" = (/2)* + (Q* =

= (3)* + (5)* = 81 + 625= 706; Мгщ = (3+ 1)* + 1 = 257.

Следовательно, для звездной структуры верхняя оценка Nx увеличилась в 1,2 раза, а нижняя Nin возросла в 14 раз.

Увеличение количества ДНС для произвольных СВК усложняет выделение характерных неисправностей и снижает эффективность использования результатов контроля при диагностировании системы. Кроме того, при большом количестве дне требуются большие объемы памяти и время обработки результатов контроля, что существенно влияет на стоимость и Бремя поиска неисправностей в системе.

При отсутствии данных о взаимном контроле для л = 13 элементов каждый из элементов может произвольно принимать состояние исправен или неисправен. Поэтому общее количество дне в данном примере составит N = 2 = 8192. Следовательно, звездные структуры обеспечивают сокращение количества ДНС в Wn= N/Nm.x = 8192/706 =11,6 раз.

В результате при анализе неисправностей в системе даже для самого неблагоприятного случая максимальных структур существенно сокращается объем вычислений или требуемый объем памяти по сравнению с цепочными структурами.

Рассмотрим кольцевые структуры.

Лемма 7, Для кольцевых структур минимальное количество дне равно 2, а максимальное (f„ i -f /„ з), где п - общее количество элементов, л > 3.

Из рассмотренного ранее следует, что любая цепочка элементов, отличная от минимальной структуры, будет иметь большее количество ДНС. Поэтому рассмотрим минимальные структуры. Установим связь между первым и последним элементами цепочки и проанализируем, при каких значениях связи количество ДНС будет минимальным, а затем рассмотрим СВК с минимальными ДНС.

Для первого случая (рис. 15, а) при присвоении произвольному элементу состояния 1 все остальные элементы получают состояние 1, а при присвоении О -состояние 0. В этом случае элементы могут быть либо все исправные, либо все неис-

Vs V, v„.i Yn

П -i -J У »/7v f/7

V, Уг Vj V„., V„ V, IV Vj V, V„

V, Vz Vj V„-, V„ V, Уг Vj V,.! v„., v„

Рис, 15. Синдромы кольцевых структур

правные, т. е. N == 2. Для определения состояний всех элементов достаточно установить исправность хотя бы одного.

Во втором случае (рис. 15, б) при исправности одного элемента все остальные элементы исправны, а в случае его неисправности допустимыми являются все п наборов неисправностей, т. е. общее количество ДНС составляет п 1 как и для минимальных структур. Следовательно, введение такой связи не оказывает практически влияния на количество и состав ДНС. Таким образом, минимальное количество ДНС для кольцевых структур равно 2, что можно использовать при диагностировании системы. Учитывая, что отказ всех элементов кольцевой структуры является маловероятным, достаточно просто устанавливается, что элементы этой структуры работоспособны. С этой целью между элементами кольцевой структуры устанавливаются однонаправленные связи. При получении результатов контроля «исправен» по всем связям можно с достоверностью говорить об исправности этих элементов.