Описанный алгоритм показан на рис. 16. Время вычисления допустимого набора неисправностей по данному алгоритму пропорционально произведению наибольшего количества неисправных элементов t и количества дуг m = \Е\.

Оценим быстродействие Начат ) Рис. 16. Алгоритм алгоритма В Случае отсут-Г днагностироваиия без ствия взаимонаправленных Босстановлеиия .3,3 оддго элемента к другому. Максимально допустимое количество неисправностей t удовлетворяет условию <: L(« - 1)/2J, а т -условию т<: <: (п - 1)«/2. Тогда при п > 1 максимальное время вычисления допустимого набора неисправностей можно оценить как

В качестве Су выбирают константу, определяемую максимальным временем вычисления одного набора неисправностей.

Если алгоритм не используется, то для вычисления всех дне необходим полный перебор состояний элементов У структуры G = G (У, Е), с проверкой допустимости каждого из получаемых наборов состояний при заданном синдроме. В этом случае максимальное время поиска дне оценивается как

W2 82".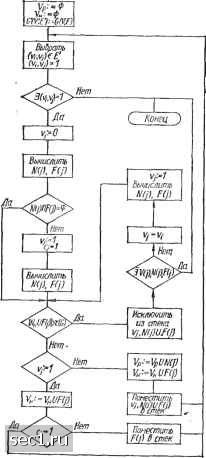

Здесь в качестве также выбирают константу, соответ ствующую времени получения одного набора неисправностей.

Таким образом, при испльзовании алгоритма 1 удается сиизить максимальное время поиска приблизительно в р =

WJW, раз, т. е.

P-(c2/ci)(4.2"/n«) ==Сз2"/п«,

где Сз = 4С2/С1.

При условии Ci= С2 (время цикла вычисления одинаково) и значениях п = 10,20 выигрыш по быстродействию р составляет приблизительно 4 и 500.

Таким образом, при V > 10 применение алгоритма позволяет существенно сократить максимальную оценку времени вычисления допустимого набора неисправностей.

В практике построения отказоустойчивых мультимикро-процессорных систем при наличии развитой системы связи отдельных ЭМ между собой представляется возможным введение новых, заведомо исправных микропроцессоров или микро-ЭВМ. Путем достаточно простых операций переадресации вновь вводимые элементы могут занять место неисправных элементов СВ1<. Неисправности в таких восстанавливаемых системах определяются путем последовательного обнаружения одного или более неисправных элементов на каждом этапе диагностирования с последующей заменой их на исправные. В результате значительно упрощаются не только алгоритмы контроля и диагностирования, но и сокращается время определения дне . При этом возможно диагностирование гораздо большего количества неисправных элементов, чем в случае структур без восстановления.

Рассмотрим алгоритм диагностирования с восстановлением для СВК, описываемых моделями Р, В, R. Обобщенная модель тестирования для этих трех моделей структур является R-ыо-дель, для которой имеются наборы полных тестов h, h, .... /1 для элементов v, v, ... , vV, причем предполагается, что для произвольного набора элементов у.,

Vj, ... , Vk полные тесты h ({о,-, о/.....ь]) являются

объединениями полных тестов h{v, h(v для отдельных элементов, т. е.

h{{vi, Vi, ...,Vk})h(о,) и h(о,) и h(t;,-) U • • • [} h{v„).

Назовем агрегатированным синдромом упорядоченное множество а = (01, а, .... о„>, где о, -общее число тестов для Vi, которые не проходят (дают результат неисправен) при данном множестве тестов h, . • • , h.

Рассмотрим простейшие алгоритмы диагностирования по агрегатированным синдромам с использованием полной или частичной замены элементов структуры 155].

Алгоритм 2.

1. Определить агрегатированный синдром а для множества тестов hx, hn-

2. Если F = [t;,0/ ФО я V/ ие заменен] = 0, то система считается исправной и процесс диагностирования окончен. В противном случае заменить все элементы в F и перейти к шагу 1.

Алгоритм 3.

1. Определить агрегатированный синдром о для множества тестов hi, hm.

2. Определить F = г/1 а, О и v/ не заменен]. Если F- 0, то система считается исправной и диагностирование окончено. В противном случае выбрать

F = {o,t;,6f :Vt;,-6f. а, > оу].

3. Заменить все элементы в F и перейти к шагу 1. Алгоритм 2 состоит в замене всех элементов структуры при

наличии, по крайней мере, одного результата непрохождения теста.

В алгоритме 3 замене подлежат последовательно все элементы, для которых число непрошедших тестов является наибольшим. Алгоритм можно естественно обобщить на случай замены нескольких элементов. Множество F в этом случае следует выбирать исходя из фиксированного наибольшего количества элементов s

F = {Vk\VkF и Vvj Фи„ ь¥:оФ0. Оа>СТ/, Аб(г, .... г -s)}.

.В реальных системах реализация тестов (й, й„) сопряжена с использованием элементов (о, о„), неисправность которых может привести к искажению отдельных тестов.

Поэтому для всех множеств тестов Г (о,.), в формировании которых принимает участие элемент о, возможно искажение получаемых синдромов, т. е. множеств результатов контроля. При симметричном искажении теста /г,- б Т ipD тест hj G h (о,) может проходить (выдается результат «исправен») даже при неисправности о,-. При несимметричном искажении тест hj не проходит (например, выдается результат «неисправен») при исправности элемента Vj.

Таким образом, для случаев симметричного и несимметричного искажений теста алгоритмы 2 и 3 приводят к полному восстановлению систем при любых состояниях работоспособности элементов системы перед началом диагностирования. При этом время вычисления по данным алгоритмам пропорционально количеству тестов m и количеству практически неисправных элементов t- Некоторое повышение быстродействия алгоритмов возможно за счет исключения из проверки тестов, проверяющих функционирование восстановленных (замененных) Элементов структуры