взаимно однозначное соответствие между вершинами графов, при котором сохраняютвя соотношения инцидентности вершин множества V, то их множества допустимых структур выбирают СВК с наименьшими показателями стоимости и наибольшими показателями эффективности. В соответствии с выражением (4.1) алгоритм получения /-диагностируемых без восстановления СВК имеет следующий вид:

1. Принять б равным 0.

2. Вычислить б = б -f- 1.

3. Если 6 = п, то конец. Все структуры перечислены. Если б < /г, то перейти к следующему шагу.

4. Определить наибольший общий делитель чисел б и /г.

5. Если наибольший общий делитель больше единицы, то перейти к шагу 2. В прогивном случае перейти к следующему шагу.

6. Вычислить и выдать структуру взаимоконтроля, удовлетворяющую заданным значениям б, / и п.

7. Перейти к шагу 2.

Шаг 4 может быть выполнен, например, с использованием алгоритма Евклида, а шаг 6 алгоритма - перебором допустимых связей при заданных б, /, п.

На рис. 18,а показан общий вид предложенного алгоритма, а на рис. 18,6 - реализация, соответственно, алгоритма и для шага 6 построения структур.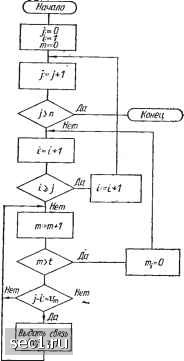

Рис. 19. Алгоритм построения структур с восстановлением

Евклида для шага 4 Здесь через d обозначен наибольший общий делитель для б и п, а с = г (А/В) - остаток от деления А на В.

Простота алгоритма обеспечивает быстрое построение СВК при проектировании системы и при перестройке по результатам диагностирования и восстановления в процессе эксплуатации. В ряде случаев оказывается целесообразно строить СВК с ограниченным числом связей.

Обозначим наибольшее количество связей, которые могут иметь Элементы Uj, v, ...,Vn£V, входящие в v, через dj.

а выходящие - через d], тогда СВК могут быть построены первоначально для

dmax - max d] и di = min dj (4.2)

/-=1.....n /=1.....n

с последующим дополнением оставшихся связей между остальными элементами. При построении диaгнocтиpyeмыx СВК с восстановлением наиболее просто использовать кольцевые структуры, для которых условие диaгнocтиpyeмocти имеет следующий вид 1411:

п> 1+(«+1)2 + ?.(т + 1), (4.3)

где т - целое число; = 2т + Я, и Я, принимает значение О или 1.

Для заданного числа п наибольшее t может быть определено следующим образом. Перебирая значения т = 1,2, ... находят первое из них, удовлетворяющее соотношению (4.3) при X = 0,1. Полученное значение сравнивается с наибольшим заданным для системы /max- Если требования диaгнocти-руемости с восстановлением не удовлетворяются (jt < tmax), то дополняем кольцо новыми связями в следующем порядке. Выбираем элементы, которые могут иметь не меньше, чем 2/-1 связей, и образуем связи со смежными с ними 2t - 2 элементами. Алгоритм, поясняющий принцип построения таких СВК. показан на рис. 19.

3. СИНТЕЗ ПЕРЕСТРАИВАЕМЫХ СТРУКТУР

Преимущества отказоустойчивых систем в наибольшей степени проявляются в возможности непрерывного достоверного функционирования. Можно выделить два способа контроля и диагностирования: путем проверки элементов, выполняющих основные функции (функциональный контроль и диагностирование), и путем перевода подмножеств проверяемых элементов в режим диагностирования. Проверенные исправные элементы во втором случае «возвращаются» в состав элементов, выполняющих основные функции-

При втором способе не требуется разделение времени работы одних и тех же элементов для выполнения основных и контрольных функций. В результате упрощается программное обеспечение и алгоритмы контроля и диагностирования. Последовательная проверка элементов системы в этом случае производится путем перестройки структуры связей между элементами. В процессе такой перестройки образуются два основных подмножества элементов: контролируемых и выпол-

няющих основные функции. Часть элементов может служить в качестве резервных.

Построение структур и рациональный выбор элементов в процессе перестройки определяется конкретными требованиями к диагностированию системы. Поэтому ниже изучаются принципы построения перестраиваемых структур с учетом стоимостных параметров эксплуатации системы. Для определенности в основу перестраиваемых структур положены теоремы, полученные 138, 39] при /-диагностируемости для AL-структур 15 и.

В структурах DiL связь между элементами Vi и Vj существует лишь в том случае, когда выполняется равенство / - / = = mod п, n = \V\ СВК. Рассмотрим первоначально случай диагностирования без восстановления.

Теорема 14. В Z)ii,-cTpyKTypax при исключении произвольных В элементов (1 <. В L - I) обеспечивается /-диагностируемость без восстановления, где

/=:min[L-е, Цп - В- 2)/2]}.

Следовательно, с увеличением количества В элементов системы, используемых для решения основных задач, снижается число обнаруживаемых неисправных элементов. Вместе с тем повышается эффективность работы системы за счет использования этих элементов по своему прямому назначению.

Обозначим через /к время диагностирования с помощью СВК- Предположим, что период между очередными профилактическими проверками равен to- Полагая, что стоимость работы элемента системы в единицу времени составляет ci. стоимость эффекта от работы элемента системы Cg, получаем ориентировочную оценку для показателя эффективности вычисления системы в течение периода to-

Wo = ПС (/о - /к) - (П - В) Ci/k-

При полном исключении элементов системы на время контроля от выполнения основных функций возможно некоторое снижение значения времени tK РР значения /«. Показатель эффективности системы в этом случае будет иметь вид

Wl = nCj (/о - /к) - nci/к.

Можно определить также нормированный показатель эффективности К системы, который равен отношению показателя Wo системы к показателю Wi, т. е.

0 , «"2 {tv - Q -{п+В) ct